Speaker: Hiroshi Matsuzoe (Nagoya Institute of Technology, Japan)

Title: Geometry of affine distributions and pre-geometric divergences

Abstract: Affine differential geometry, the geometry of statistical manifolds, and information geometry are closely related. The basic structures that appear in the geometry of statistical manifolds and information geometry were already described in Blaschke's textbooks 100 years ago. However, in information geometry, the rediscovery of conjugate connections has made great progress, including applications.

In this talk, we will review the relationship between affine differential geometry and information geometry. After that, we present recent results on the geometry of affine distributions and geometric pre-divergences.

Speaker: Barbara Opozda (Jagiellonian University, Poland)

Title: On the geometry of the tangent and sphere bundles over statistical manifolds

Abstract: A statistical structure on a manifold M induces a Riemannian metric (called the Sasakian metric) on the tangent bundle TM. The metric is rigid in the following sense: if its scalar curvature is bounded from below, then the statistical connection must be flat. The situation is quite different, when we consider the induced metric on the sphere bundles. In particular, we have: for a sufficiently small radius of a sphere bundle over a compact statistical manifold (with any statistical structure) of dimension greater than 2, its scalar curvature is greater than any prescribed number.

Speaker: Hideyuki Ishi (Osaka Metropolitan University, Japan)

Title: The Jorgensen set for transitive exponential families

Abstract: It is well-known that the Kullback-Leibler divergence for an exponential family coincides with the Bregman divergence associated to the cumulant function. However, an arbitrary Bregman divergence is not always realized as the Kullback-Leibler divergence. In other words, an arbitrary convex function is not always equal to a cumlant function. Let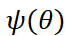 be the cumulant function of an exponential family. In 1987, Jorgensen considered the set of 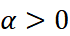for which 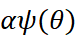is again the cumulant function of some exponential family. For instance, the family of 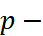dimensional centered Gaussian distribution is an exponential family with natural parameter being the concentration matrix 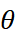. Then the cumulant function is 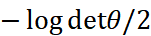In this case, the set of the parameter 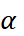is the union of the discrete part 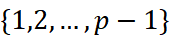and the continuous part 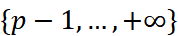. This set appears in various areas of mathematics and called by different names such as Berezin-Wallach set and Gindikin set. In this talk, we determine the Jorgensen set for every exponential family that admits transitive group action on the parameter space. Moreover, we discuss the meaning of the Jorgensen set from the viewpoint of Kähler geometry.

Speaker: Michel Nguiffo Boyom (Alexander Grothendieck Research Institute, France)

Title: TBA

Abstract: TBA

Speaker: Zejun Hu (Zhengzhou University, China)

Title: Recent progress on the study of affine hypersurfaces

Abstract: In this lecture, we talk about several important advances in geometry of affine hypersurfaces. This mainly includes the study of affine maximal hypersurfaces, the affine hypersurfaces with constant affine Gauss-Kronecker curvature, the affine hypersurfaces with parallel Fubin-Pick form in equiaffine differential geometry as well as some related results in centroaffine differential geometry.

Speaker: Giovanni Pistone (Collegio Carlo Alberto, Italy)

Title: Affine Geometry of the Statistical Bundle

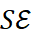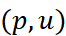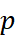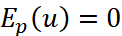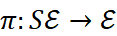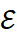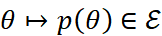Abstract: The Statistical Bundle is the set of couples with strictly positive probability function and a real random variable such that . It is a vector bundle where is the open probability simplex on a finite set. For example, if is a smooth one-dimensional probability model, the lift 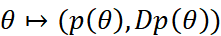is a smooth curve in the Statistical Bundle, where 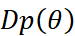is the Fisher's score (logarithmic derivative) of the model.

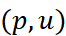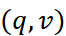Given two points and in 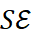, one can define affine displacements in the elementary sense of Weyl (1921),

,

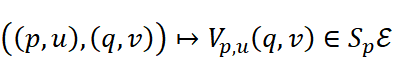and correspondingly define an affine geometry on the Statistical Bundle. The further assignment of a duality pairing on the fibres produces by dualization a dually flat geometrical structure. See a tutorial in G Chirco and G Pistone arXiv:2204.00917.

Defining the affine geometry on the Statistical Bundle implicitly defines the connection on the non-parametric affine bundle of the open probability simplex.

The study of Information Geometry of the Statistical Bundle has other distinct advantages—first, a simplified presentation of the transport Problem of the probability simplex. See G. Pistone. Statistical bundle of the transport model. In GSI 5th Proceedings, 752–759. Springer-Verlag, 2021. Second, the vector bundle and its dual provides the proper setting for studying Lagrangian and Hamiltonian mechanics of the probability simplex. See G Chirco, L Malagò, G Pistone. Lagrangian and Hamiltonian dynamics for probabilities on the statistical bundle. International Journal of Geometric Methods in Modern Physics, 19(13):2250214.1–46, August 2022.

The talk will mention other relevant references, particularly the generalization to continuous state space. My presentation will mainly focus on the statistical meaning of geometric concepts.

Speaker: Gabriel Khan (Iowa State University, USA)

Title: Statistical Mirror Symmetry

Abstract: In complex and symplectic geometry, mirror symmetry is a duality between Calabi-Yau manifolds, in which two distinct spaces have closely related geometry. This idea has played an important role in string theory as well as enumerative algebraic geometry. In this talk, we will discuss a related duality known as statistical mirror symmetry. For any exponential family, this theory provides a relationship between two canonical Kähler geometries defined on the tangent bundle of the associated statistical manifold. Our focus will be the family of normal distributions, where statistical mirror symmetry gives a correspondence between the unit ball in ℂ2 and the Siegel-Jacobi space. Finally, we will discuss how this theory relates to Kähler-Ricci flow and a conjectural application in number theory.

Speaker: Shin-itiro Goto (Chubu University, Japan)

Title: Affine geometric description of thermodynamics

Abstract: Thermodynamics is a branch of physics that offers systematic approaches

to analysing thermodynamic phenomena. Despite its success, its mathematical description is expected to be clearer. To formulate thermodynamics in the language of sophisticated mathematics, thermodynamics is described by a variety of differential geometries, including contact and information geometries. Meanwhile, affine geometry is a branch of differential geometry and is compatible with information geometry. By combining above, it is expected that thermodynamics is compatible with affine geometry, and it is expected that several affine geometric tools can be introduced in the analysis of thermodynamic systems. In this talk, we show a set of affine geometric descriptions of thermodynamics, and then we show a comparison with a contact geometric description.

Speaker: Hao Xu (Zhejiang University, China)

Title: Frobenius algebra structure of statistical manifold

Abstract: A statistical manifold is a Riemannian manifold (M,g) equipped with a totally symmetric (0,3)-tensor. We show that the tangent bundle of a statistical manifold has a Frobenius algebra structure if and only if the sectional K-curvature vanishes. The sectional K-curvature was introduced by Opozda and has analogous properties of Riemannian curvature. As a natural generalization of WDVV equation, an interesting question is to classify statistical manifold with constant sectional K-curvature. This is joint work with Kefeng Liu and Yanhui Zhi.

Speaker: Koichi Tojo (RIKEN Center for Advanced Intelligence Project, Japan)

Title: Harmonic exponential families on homogeneous spaces

Abstract: Exponential families play a significant role in the field of information geometry and are useful in Bayesian inference. Widely used families of probability measures, such as normal and gamma distributions can be considered as exponential families on homogeneous spaces with symmetry. Based on this observation, we presented a method to construct exponential families with symmetry using representation theory. In this talk, we will explain the method and its properties, illustrating them with examples.

Speaker: Xinyue Cheng (Chongqing Normal University, China)

Title: Some inequalities and gradient estimates for harmonic functions on Finsler measure spaces

Abstract: In this talk, we study functional and geometric properties on complete Finsler measure spaces with weighted Ricci curvature Ric_∞bounded below. We first obtain some local uniform Poincare inequalities and Sobolev inequalities. Further, we give a mean value inequality for nonnegative subsolutions of elliptic equations. Based on these, we obtain local and global Harnack inequalities for positive harmonic functions. Finally, we establish a global gradient estimate for positive harmonic functions on forward complete non-compact Finsler measure spaces. Besides, as a by-product of the mean value inequality, we prove a Liouville type theorem.

Speaker: Weiping Zhang (Nankai University, China)

Title: Dirac operators and scalar curvature

Abstract: We will describe some applications of Dirac operators to the existence of metrics of positive scalar curvature.

Speaker: Ruiwei Xu (Henan Normal University, China)

Title: Classification of Calabi hypersurfaces with parallel Fubini-Pick form

Abstract: The classifications of locally strongly convex equiaffine hypersurfaces (resp. centroaffine hypersurfaces) with parallel Fubini-Pick form with respect to the Levi-Civita connection of the affine metric (resp. centroaffine metric) have been completed by Hu-Li-Vrancken, Cheng-Hu-Moruz et al in the last decades. In this talk, I shall show classifications of Calabi hypersurfaces with parallel Fubini-Pick forms in any dimensions. This talk is based on the joint work with Dr. Miaoxin Lei.

Speaker: Guangyue Huang (Henan Normal University, China)

Title: Reilly type integral formulas and some related applications

Abstract: We will recall some Reilly type integral formulas. As some applications, for Reilly type integral formula on the weighted measure space or those associated with affine connections on Riemannian manifolds, we can achieve Heintze-Karcher and Minkowski type inequalities. Furthermore, we will give some eigenvalue relationships