Speaker: 刘建玲（重庆理工大学）
Time: 14:30-15:30, Dec. 4 2024
Venue: 数学中心研讨室（至善楼602）
Title: 双曲空间中常数量曲率超曲面的刚性
Abstract:
Assume that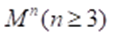 
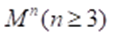is a complete hypersurface in H^(n+1) with constant scalar
curvature R=n(1-n). Assume that B,H,g is the second fundamental form, the mean curvature and the induced metric of M, respectively. We prove that M is totally geodesic if
(1)
for some positive constant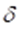 
, where
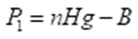which denotes the first order Newton
transformation,
(2)
and
(3)
for some small enough positive constant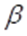 
which depends only on 
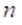and .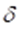
Speaker: 李智（河南师范大学）
Time: 14:00-15:00, Nov. 27 2024
Venue: 数学中心研讨室（至善楼602）
Online: Zoom: 811 5638 1768（Password: msrc）
Title: The rigidity problems of complete self-similar solutions to the mean curvature flow
Abstract:
Self-shrinkers play an essential role in understanding the behavior of mean curvature flow at singular time. In this talk, I will give a survey about the classification problems of complete self-shrinkers. Then I will talk about rigidity of complete Lagrangian self-shrinkers with the constant the norm of the mean curvature vector and extend this research method to Lagrangian self-expander. This talk is based on my joint papers with Prof. Guoxin Wei and Dr. Ruixin Wang.
Speaker: 曹蕾（河南大学）
Time: 10:00-11:00, Nov. 6 2024
Venue: 数学中心研讨室（至善楼602）
Online: Zoom: 811 5638 1768（Password: msrc）
Title: Soliton solutions arising in Gauge Field Theories and its application
Abstract:
In this talk, we will present a series of solitons arising in several gauge field theory models. In the context of the Abelian gauge field theory, we unveil the surprising result that the solutions may explicitly be constructed, which enriches our knowledge on integrability of the planar Liouville type equations in their one-dimensional limits. We also construct self-dual vortices and cosmic strings from the generalized Abelian Higgs theory. A number of properties of the vortices and strings are also established
Speaker: 李玉巧（合肥工业大学）
Time: 10:00-11:00, Oct. 28 2024
Venue: 数学中心研讨室（至善楼602）
Title: Stability of the area preserving mean curvature flow
Abstract:
In this talk, we consider the long-time existence and convergence of the area preserving mean curvature flow of hypersurfaces in space forms under some initial integral pinching conditions. More precisely, we prove that the flow exists for all time and converges exponentially fast to a totally umbilical sphere if the integral of the traceless second fundamental form is sufficiently small. Moreover, we show that starting from a sufficiently large coordinate sphere, the area preserving mean curvature flow exists for all time and converges exponentially to a constant mean curvature surface in asymptotically Schwarzschild spaces. This work is joint with Dr. Yaoting Gui and Pf. Jun Sun.
Speaker: 韩英波 (信阳师范大学)
Time: 16:00-17:00, Oct. 28 2024
Venue: 数学中心研讨室（至善楼602）
Online: Zoom: 811 5638 1768（Password: msrc）
Title: The uniformization conjecture in complete non-compact Sasakian manifolds
Abstract:
The CR analogue of Yau uniformization conjecture states that any complete noncompact Sasakian manifold of positive CR holomorphic bisectional curvature is CR biholomorphic to the standard Heisenberg group. In this talk, we affirm the partial result of the above conjecture on Sasakian manifolds by using Sasaki-Ricci flow. More precisely, we show that a complete noncompact Sasakian manifold M^(2n+1) of bounded nonnegative transversal bisectional curvature with maximal volume growth is CR biholomorphic to 𝛺 × ℝ, where 𝛺 is a pseudoconvex domain of ℂ .
Speaker: 张世金 （北京航空航天大学）
Time: 16:00-17:00, Oct. 24 2024
Venue: 数学中心研讨室（至善楼602）
Online: Zoom: 811 5638 1768（Password: msrc）
Title: A quantitative second order estimate for p-harmonic functions on Riemannian manifolds
Abstract:
In this talk, first I will introduced some results about the gradient estimate of p-harmonic functions on Riemannian manifolds, including the results of Kotschwar-Ni, Wang-Zhang, Sung-Wang. Then I will introduce the results about the quantitative second-order Sobolev estimate of for positive p-harmonic functions in Riemannian manifolds under Ricci curvature bounded from below and also for positive weighted p-harmonic functions in weighted manifolds under the Bakry-Émery curvature-dimension condition. This is a joint work with Jiayin Liu and Yuan Zhou.
Speaker: 张良迪 (北京雁栖湖应用数学研究院)
Time: 14:00-15:00, Oct. 16 2024
Venue: 数学中心研讨室（至善楼602）
Online: Zoom: 811 5638 1768（Password: msrc）
Title: New curvature characterizations of spherical space forms and complex projective spaces
Abstract:
In this talk, we introduce a new positivity notion for curvature of Riemannian manifolds and obtain characterizations for spherical space forms and the complex projective space. This is a joint work with Prof. Xiaokui Yang.
Speaker: 陈航（西北工业大学）
Time: 10:00-11:00, Oct. 10 2024
Venue: 数学中心研讨室（至善楼602）
Online: Zoom: 811 5638 1768（Password: msrc）
Title: On the Morse index of minimal submanifolds
Abstract:
In this talk, firstly I will review some topics on the Morse index of minimal submanifolds, including the gap phenomena and estimates of index and related classification result. Then I will present my recent work on the nonexistence of minimal submanifolds in some Riemannian manifolds, which is related to the famous Lawson-Simons conjecture.
Cirriculum Vitae:
陈航，西北工业大学数学与统计学院副教授，硕士生导师；2004-2013年在清华大学数学科学系学习，先后获理学学士和理学博士学位；2017-2018 年以访问学者身份赴美国加州大学圣塔芭芭拉分校进行学术交流合作;主要研究领域为子流形几何和黎曼流形的特征值问题；主持国家自然科学基金1项，陕西省自然科学基金2项；以独立作者身份获陕西省第十五届自然科学优秀学术论文奖三等奖；在Calc. Var. PDE, J. Geom. Anal., Sci. China Math., Potential Anal., Bull. Lond. Math. Soc.等期刊发表论文10余篇。
Speaker: 赵唯 (华东理工大学)
Time: 14:00-15:00, Sep. 19, 2024
Venue: 数学中心研讨室（至善楼602）
Online: Zoom: 811 5638 1768 （Password：msrc）
Title: Functional inequalities on Riemannian-Finsler manifolds
Abstract:
In this talk, we consider the validity of functional inequalities on Riemannian-Finsler manifolds. In particular, we establish surprising analytic aspects of Finsler manifold. That is, Hardy inequality, Heisenberg-Pauli-Weyl uncertainty principle and Caffarelli-Kohn-Nirenberg inequality usually hold under the non-positive S-curvature condition while fail under the positive S-curvature condition.
The talk is based on the joint work with Alexandru Kristály and Benling Li.
Speaker: 熊昌伟 (四川大学)
Time: 16:10-17:10, May. 27, 2024
Venue: 数学中心研讨室（至善楼602）
Online: Zoom: 811 5638 1768 （Password：msrc）
Title: A weighted Reilly formula for differential forms and sharp Steklov eigenvalue estimates
Abstract:
In the talk first we will present how to establish a weighted Reilly formula for differential forms on a compact Riemannian manifold with boundary. Then we give some applications of this formula. One is a sharp lower bound for the first positive eigenvalue of the Steklov eigenvalue problem on differential forms investigated by Belishev and Sharafutdinov (2008) and Karpukhin (2019). A second one is a comparison result between the spectrum of this Steklov eigenvalue problem and the spectrum of the Hodge Laplacian on the boundary of the manifold. At the end we discuss an open problem for differential forms analogous to Escobar's conjecture (1999) for functions. The talk will be mainly based on the preprint arXiv:2312.16780v2.
Speaker: 张树城 (msrc)
Time: 16:10-17:40, Apr. 22, 2024
Venue: 数学中心研讨室（至善楼602）
Online: Zoom: 811 5638 1768 （Password：msrc）
Title: Bernstein-Type Theorem for Entire Special Lagrangian Graph II
Abstract:
We will talk about the structure theory for entire minimal graph of higher codimensions. In particular, we will focus on the Berstein-type theorem for special Lagrangian graph. This is based on papers by Yuan and Ding. At the end, some related problems are addressed.
Speaker: 张树城 (msrc)
Time: 16:10-17:40, Apr. 15, 2024
Venue: 数学中心研讨室（至善楼602）
Online: Zoom: 811 5638 1768 （Password：msrc）
Title: Bernstein-Type Theorem for Entire Special Lagrangian Graph I
Abstract:
We will talk about the structure theory for entire minimal graph of higher codimensions. In particular, we will focus on the Berstein-type theorem for special Lagrangian graph. This is based on papers by Yuan and Ding. At the end, some related problems are addressed.
