每周四10:30-12:00, 2022.09-2023.01
Zoom Meeting（ID: 84374140142& Password: 202209）
Speaker: Li Sheng (Sichuan University)
Time: 10:30-12:00, January 12, 2023
Venue: Online (Zoom Meeting ID: 84374140142 & Password: 202209)
Title: Extremal Metrics on Toric Manifolds
Abstract:
An example of Apostolov et al. indicates that the condition of K-stability may not be correct one for general polarized manifolds. Székelyhidi modified definition of K-stability by filtration and stated a variant of the Yau-Tian-Donaldson conjecture. We will give an introduction to extremal metrics and K-stability, and talk about our results on this variant of YTD conjecture for toric manifolds. This is jointed with Li An-Min and Lian Zhao.
Speaker: Jun Sun (Wuhan University)
Time: 10:30-12:00, January 6, 2023
Venue: Online (Zoom Meeting ID: 84374140142 & Password: 202209)
Title: Curve shortening flow in a 3-dimensional pseudohermitian Manifold
Abstract:
In this talk, we introduce a curve shortening flow in a 3-dimensional pseudohermitian manifold with vanishing torsion. The flow preserves the Legendrian condition and decreases the length of curves. The stationary solution of our flow is a Legendrian geodesic. We classify the singularity and prove some convergence results. Moreover, we study the flow in Heisenberg group especially with Type I singularity. This talk is based on joint work with Shujing Pan.
Speaker: Fangyang Zheng, Chongqing Normal University
Time: 10:30-12:00, January 5, 2023
Venue: Online (Zoom Meeting ID: 84374140142 & Password: 202209)
Title: Hermitian manifolds: when Chern connection is Ambrose-Singer
Abstract:
This talk is based on joint work with Prof. Lei Ni of UCSD. We will discuss the geometry of a special type of locally homogeneous Hermitian manifolds: those whose Chern connection is Ambrose-Singer, namely with parallel torsion and curvature. We will show that the universal covering spaces of such manifolds are always the product of Hermitian symmetric spaces and complex Lie groups.
Speaker: 周恒宇 副教授（重庆大学）
Time: 10:30-12:00, December 22, 2022
Venue: Online (Zoom Meeting ID: 84374140142 & Password: 202209)
Title: The Dirichlet problem of a class of prescribed mean curvature equations in Riemannian manifolds
Abstract:
In this talk we discuss the Dirichlet problem of a class of prescribed mean curvature (PMC) equations in Riemannian manifolds. Its solution gives a PMC graph in product manifolds whose mean curvature has zero derivatives concerning the height. Inspired by Schoen-Yau's blow-up method in the proof of positive mass theorems, we proposed an Nc-f property. Under the Nc-f property and a natural boundary condition, a blow-up process of auxiliary Dirichlet problems will yield the solution of the corresponding Dirichlet problems.
Speaker: Botong Xu
Time: 10:30-12:00, December 15, 2022
Venue: Online (Zoom Meeting ID: 84374140142 & Password: 202209)
Title: Hyperbolic p-sum and horospherical p-Brunn-Minkowski theory in hyperbolic space
Abstract:
In this talk, for any positive number p, we introduce a sum of two sets in hyperbolic space, and we call it the hyperbolic p-sum. Then we develop a Brunn-Minkowski theory in the hyperbolic space by use of our hyperbolic p-sum, and we call it the horospherical p-Brunn-Minkowski theory. We will talk about some progress on the central problems in this theory, including the horospherical p-Minkowski problem, the horospherical p-Christoffel-Minkowski problem, the horospherical p-Brunn-Minkowski inequality, and the horospherical p-Minkowski inequalities. This talk is based on joint work with the supervisor Haizhong Li, arXiv: 2211.06875.
Speaker: 赵恩涛
Time: 10:30-12:00, December 8, 2022
Venue: Online (Zoom Meeting ID: 84374140142 & Password: 202209)
Title: Convergence and rigidity theorems for the mean curvature flow
Abstract:
We will talk about smooth convergence and rigidity theorems for the mean curvature flow of arbitrary codimension. We first give a brief survey on the geometry and topology of submanifolds in space forms. Then we will discuss the smooth convergence for mean curvature flow of arbitrary codimension under certain curvature pinching conditions. At last, we will present several rigidity theorems for ancient solutions of the mean curvature flow. This talk is based on the joint works with Prof. Kefeng Liu, Prof. Hongwei Xu, Dr. Li Lei and other collaborators.
Speaker: Jiazu Zhou
Time: 10:30-12:00, November 24, 2022
Venue: Online (Zoom Meeting ID: 84374140142 & Password: 202209)
Title: Isoperimetric problem from viewpoint of integral and convex geometry
Abstract:
Mathematics roots back to the classical isoperimetric problem. The known isoperimetric problem says that the ball has maximum volume among all geometric figures with the presumed perimeter (measure). Recent research and applications in geometry, analysis, PDE showed more basic connections between the isoperimetric problem and Brunn-Minkowski theory. We will address some recent works on these problems, especially solved by Chinese geometers.
Speaker: Hongbing Qiu
Time: 10:30-12:00, November 17, 2022
Venue: Online (Zoom Meeting ID: 84374140142 & Password: 202209)
Title: Rigidity of self-shrinking surfaces and its applications
Abstract:
By the fact that a self-shrinking surface in Euclidean space R4 is hyper-Lagrangian, we prove a rigidity result of self-shrinking surfaces by restriction of the image under the complex phase map, it not only improves a corresponding rigidity theorem of symplectic self-shrinking surfaces, but also it is optimal. As applications, by using the blow-up analysis of mean curvature flows and the previous rigidity result of self-shrinking surfaces, we show that if the image of the initial closed surface under the complex phase map avoids a closed half great circle, then the corresponding mean curvature flow does not develop any Type I singularity. This restriction of the image under the complex phase map is sharp. Finally, we demonstrate that any hyper-Lagrangian submanifold L2n(n > 1) in a hyperkähler manifold M4n is complex Lagrangian. This is a joint work with Dr. L. Sun.
Speaker: Fengjiang Li
Time: 10:30-12:00, November 10, 2022
Venue: Online (Zoom Meeting ID: 84374140142 & Password: 202209)
Title: Positively curved shrinking Ricci solitons are compact
Abstract:
We will talk about the paper by Ovidiu Munteanu and Jiaping Wang with the above title (JDG, 2017). They showed that a gradient shrinking Ricci soliton with nonnegative sectional curvature and positive Ricci curvature must be compact.
Speaker: Xianfeng Wang
Time: 10:30-12:00, November 3, 2022
Venue: Online (Zoom Meeting ID: 84374140142 & Password: 202209)
Title: New characterization of the Clifford torus as a Lagrangian self-shrinker
Abstract:
In this talk, we will prove that the Clifford torus S1(1) ×S1(1) is the unique compact orientable Lagrangian self-shrinker in C2 with |A|2≤2, which gives an affirmative answer to Castro-Lerma's conjecture.
References:
Ildefonso Castro and Ana M. Lerma, The Clifford Torus as a Self-Shrinker for the Lagrangian Mean Curvature Flow, IMRN No.6 (2014), pp. 1515-1527
Haizhong Li and Xianfeng Wang, New Characterizations of the Clifford Torus as a Lagrangian Self-Shrinker, JGA 27 (2017), pp. 1393-1412
Speaker: Yong Luo
Time: 10:30-12:00, October 27, 2022
Venue: Online (Zoom Meeting ID: 84374140142 & Password: 202209)
Title: Self-shrinkers of the mean curvature flow in arbitrary codimension
Abstract:
We will talk about the paper by Knut Smoczyk with the above title (IMRN, 2005). We will mainly give details of the proof of the following theorem: Let M be a compact self-shrinker in Rn. Then M is spherical if and only if H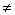
0 and its principle normal is parallel in the normal bundle.
Speaker: Chien Lin
Time: 10:30-12:00, October 20, 2022
Venue: 至善楼602 / Online (Zoom Meeting ID: 84374140142 & Password: 202209)
Title: Introduction to some basic concepts in Sasakian geometry
Abstract:
In this short course, I will very briefly survey the fundamental notions in Sasakian geometry including the definition of Sasakian manifolds, some of properties of Riemann curvature, and the related topics. All of them could be found in the book of David E. Blair, especially in Chapter 6 & 7.
Prerequisites:
Some familiarity with Riemannian manifolds. This talk is accessible to the undergraduates.
References:
David E. Blair, Riemannian geometry of contact and Symplectic manifolds (Second Edition), Birkhäuser
Ana Cannas da Silva, Lectures on symplectic geometry (Corrected 2nd printing), Springer
Speaker: Zejun Hu
Time: 10:30-11:30, October 13, 2022
Venue: Online (Zoom Meeting ID: 84374140142 & Password: 202209)
Title: On equiaffine and centroaffine hypersurfaces
Abstract:
In this lecture, I will talk about our recent research on the study of locally strongly convex affine hypersurfaces, jointed with Profs. Xiuxiu Cheng and Luc Vrancken. The results include that on both equiaffine and centroaffine hypersurfaces with canonical properties. Particularly, we classify affine hyperspheres which, in terms of the affine metric, are locally isometric to the product of two Riemannian manifolds both having constant sectional curvatures; we show that every centroaffine Tchebychev hyperovaloid is ellipsoid.
Speaker: Yingbo Han
Time: 10:30-12:00, September 29, 2022
Venue: Online (Zoom Meeting ID: 84374140142& Password: 202209)
Title: Legendrian Mean Curvature Flow
Abstract:
In this talk, we will study the Legendrian mean curvature flow in Sasakian eta-Einstein manifolds and give some convergence results for this flow. This is a joint work with Professor Shu-Cheng Chang and Chin-Tung Wu.
Speaker: Shu-Cheng Chang
Time: 10:30-12:00, September 22, 2022
Venue: Online (Zoom Meeting ID: 84374140142& Password: 202209)
Title: Foliation Divisorial Contraction by the Sasaki-Ricci Flow on Sasakian Five-Manifolds
Abstract:
Let be a compact quasi-regular Sasakian 5-manifold with finite cyclic quotient foliation singularities of type. First, we derive the foliation minimal model program by applying the resolution of cyclic quotient foliation singularities. Secondly, based on the study of local model of resolution of foliation singularities, we prove the foliation canonical surgical contraction or the foliation extremal ray contraction under the Sasaki-Ricci flow. Consequently, we have a Sasaki analogue of analytic minimal model program with the Kähler-Ricci flow due to Song-Tian and Song-Weinkove. This is a joint work with C. Lin and C.-T. Wu.
Speaker: Shu-Cheng Chang
Time: 10:30-12:00, September 15, 2022
Venue: Online (Zoom Meeting ID: 84374140142 & Password: 202209)
Title: The Legendrian Mean Curvature Flow
Abstract:
It is due to Colin-Giroux-Honda that, for fixing a Thurston-Bennequin invariant, a rotation number, and a knot type in contact 3-manifold, there are only finitely many Legendrian knot types realizing this data. However, it is proved by Ekholm-Etnyre-Sullivan that there is an infinite family of Legendrian embeddings of the n-sphere and n-torus into R²ⁿ⁺¹, n>1 that are not Legendrian isotopic even though they have the same rotation number and Thurston-Bennequin invariant.
On the other hand, it is closely related between Legendrian and Lagrangian submanifolds. More precisely, the projection of the mean curvature of a Legendrian submanifold in the contactization of a Kähler manifold coincides with the mean curvature of the projected Lagrangian submanifold in such a Kähler manifold. In particular, the projection of a minimal Legendrian submanifold is an immersed minimal Lagrangian submanifold.
Haskins has discovered examples of S¹-invariant minimal Legendrian tori in the 5-sphere by exploiting the link between S¹-equivariant conformal harmonic maps from a 2-dimensional simply connected domain into the 5-sphere and the integrable system with conserved quantities.
In this lecture, we will address the recent result on the isotopic Legendrian problem and existence of minimal Legendrian submanifolds in η-Einstein Sasakian manifolds via the Legendrian mean curvature flow which is initiated by K. Smoczyk.
